机器学习
GAN(生成式对抗网络)
什么是GAN
产生GAN的灵感来自于博弈论之中的零和博弈(zero-sum game),又称零和游戏。
与非零和博弈相对,是博弈论的一个概念,属非合作博弈。它是指参与博弈的各方,在严格竞争下,一方的收益必然意味着另一方的损失,博弈各方的收益和损失相加总和永远为“零”,故双方不存在合作的可能。
零和博弈在生活中是有很多例子:
比如打麻将,一天打下来,总是有人赢钱有人输钱,但是将赢得和输得钱加在一起正好为零,也就是说别人赢得肯定是其他人输得,其中不存在任何合作。其中有一句话说的比较能体现零和博弈:彼之所得必为我之所失。
GAN全名生成对抗网络(Generative Adversarial Networks),顾名思义,它应该是一个既有生成任务,又有对抗任务的网络。
更直白的说:就是两个新手打格斗游戏一直对打,输赢输赢,之后两个人从莽打走向了立回互摸找对手空挡的相互学习进化的过程。就是双方为了摸清对方操作手法的自我提升。
GAN的应用就十分的广泛,在各种领域中,比如医学领域中,在做病例分析和CT图判断时,由于样本过少,或者是某种病人过少,所以参考的样本比较少。为了解决这个问题,就可以使用GAN来生成人们所需要的样本模型,来帮助人类对病情进行分析。还可以运用在图片的操作上,比如图片风格迁移、超分辨率、图像补全等等。在其他领域中,可以使用GAN来生成相关的图片,用来丰富数据集。
所以生成对抗网络(GAN)有两个部分:生成网络G(Generator)和判别网络D(Discriminator)。
(1)生成网络G:用来生成图片的网络,它接收一个随机的噪声noise,通过这个噪声生成图片。
(2)判别网络D:用来判别图片是否真实的网络。它的输入是一张图片img,输出是img为真实图片的概率,如果为1,就代表100%是真实的图片,而输出为0,就代表不可能是真实的图片。
生成网络G的目的是努力生成一个图片来骗过判别网络D,判别网络D的目的是努力鉴别出生成出来的图片是假的。两个网络在不断博弈中互相进步,达到理想状态:D(G(noise))=0.5(即判别网络D也不确定是到底是不是真实的)
下面是GAN作者给出来的公式:
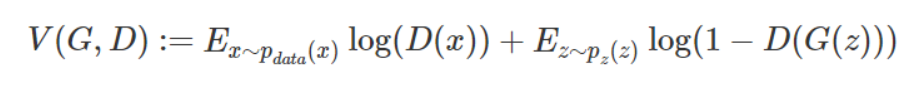
这里我们可以清晰的看出来GAN有一个生成模型,一个判别模型了。
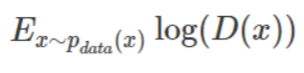
这是公式的半段,这一段是要求定义一个判别器D去判断样本原来的样子是不是从p_data(x)分布中取出来的。
E表示期望。p_data(x)表示真实数据的分布,即真实图片数据集的概率分布。对于GAN来说,生成器的目标是生成与真实数据分布相似的数据,而判别器的目标是区分真实数据和生成数据。
对于给定的输入x,判别器输出一个概率值,表示x来自真实数据集的概率。对数损失函数用于衡量判别器的预测准确性。
对于从p_data(x)中取出来的样本,我们的判别器要尽量精准的预测把它为1
其次,我们看生成器G,它的目标是努力欺骗过判别器。它是根据「负类」的对数损失函数而构建,即:
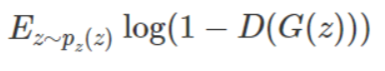
生成器G的p_z(x)表示生成数据的分布。具体来说,p_z(x)是生成器G从随机噪声z生成数据x的概率分布。这里的z是一个随机向量,通常来自一个已知的先验分布(如标准正态分布),而G是一个神经网络,将z映射到生成的数据x。
所以从式子里可以看到我们的生成器生成的虚假图像G(z),与努力把虚假图像判别为0的判别器D,即D(G(z)) = 0。
那么根据上式,我们不难想到判别器的目标是判别生成器生成的假图像,判别器的任务是使D(G(z)) ==>> 0, 而log函数是在 0~+∞上单调递增的函数,因为D(G(z)) ∈ (0, 1), 当D(G(z)) 趋向于 0, 1 - D(G(z))是单调增的。因此log(1 - D(G(z)))也是单调增的,所以我们的判别器的目标是:求其最大值。
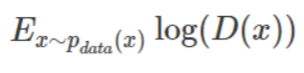
回到真实图像数据的式子,我们知道判别器努力要把来自于真实图像分布的x,判断为1,也就是D(x)=1,不难看出在判别器的视角下,这里也应该是单调递增的,所以判别器在这的目标也是求它的最大值。
既然两个式子都是求的最大值,那我们将它们结合起来,判别器的主要目标就是最大化:
当这个式子最大化的时候,代表着判别器能正确分辨真实图片与生成器生成的虚假图片。
————————————————————————————————————————————————
现在视线回到生成器,假定我们现在的判别器能正确分辨一张图片是真的图片还是生成的假图片的时候。我们给定一个生成器G,将上一步得出的当前最优的判别器表示为D*G,且定义价值函数为:
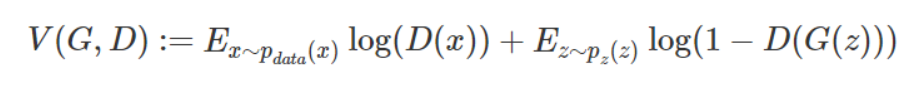
那么现在我们知道了,DG的目标是最大化V(G,D)这个函数,所以我们把DG表示为:
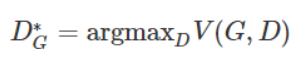
这个时候,因为前面已经获得了优的判别器,我们的生成器的目标是想要去欺骗这个判别器(开始进行对抗),那么生成器的目标就是想要D(G(z))=1。
当D(G(z))逼近于1的时候,1-D(G(z))就越来越逼近于0,那么log(1 - D(G(z)))就趋向于-∞,就单调递减,从此可以看出我们生成器的目标是:当给定了当前最优的判别器时(即D = D*G时)最小化:
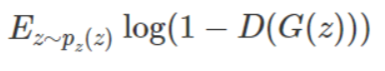
所以,我们求解G和D对抗求解极小值极大值的最优价值函数为:
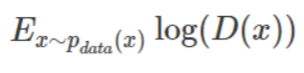
综上,我们可以看到,判别器G的目标是在给定生成器G的时候最大化整个式子(增强分辨能力),在其D最大化时,固定住判别器D(记作D*G),再最小化V(D*G,G),使其生成的数据更接近真实的数据。
(注: 我们在给定G,最大化V(D,G)的时候,此时的V(D,G)是真实图像的分布p_data 与 生成图像 P_G之间的差异或者距离。)
最后,我们的式子综合起来就可以写成下式:
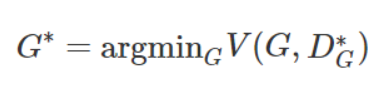
简洁总结一下:最好的生成器 = 最优情况下的判别式D*G的前提下,最小化的V(D*G, G)。
————————————————————————————————————————————————
然后就是小实验环节:
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import torchvision
from torchvision import transforms
## 对数据做归一化 (-1 1)
transform = transforms.Compose([
transforms.ToTensor(), # 0-1 : channel,high ,witch
transforms.Normalize(0.5,0.5)
])
train_ds = torchvision.datasets.MNIST('data',train=True,
transform=transform,
download=True)
dataloader = torch.utils.data.DataLoader(train_ds,batch_size=64,shuffle=True)
# 生成器 使用噪声来进行输入
# 输入为长度为100的 噪声 (正态分布随机数) 生成器输出为(1,28,28)的图片
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.main = nn.Sequential(
# 输入层到隐藏层1
nn.Linear(100, 256),
nn.ReLU(),
# 隐藏层1到隐藏层2
nn.Linear(256, 512),
nn.ReLU(),
# 隐藏层2到输出层
nn.Linear(512, 28 * 28),
nn.Tanh()
)
def forward(self, x): # x 表示为长度为100 的噪声
"""
前向传播函数,将噪声通过生成器网络生成图片
:param x: 输入的噪声,形状为 (batch_size, 100)
:return: 生成的图片,形状为 (batch_size, 1, 28, 28)
"""
img = self.main(x)
img = img.view(x.size(0), 1, 28, 28)
return img
# 判别器的实现 输入为一张(1,28,28)图片 输出为二分类的概率值,输出使用sigmoid激活 0-1#
# 是用BCELoss损失函数
# 判别器一般使用 LeakyReLu 激活函数
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.main = nn.Sequential(
nn.Linear(28*28,512),nn.LeakyReLU(),
nn.Linear(512,256),nn.LeakyReLU(),
nn.Linear(256,1),nn.Sigmoid()
)
def forward(self,x): # x 为一张图片
x = x.view(-1,28*28)
x = self.main(x)
return x
epochs = 100
lr = 0.0001 //学习率
# 初始化模型
device = 'cuda' if torch.cuda.is_available() else 'cpu'
generator = Generator().to(device)
discriminator = Discriminator().to(device)
# 优化器(梯度下降)
g_optim = torch.optim.Adam(generator.parameters(),lr=lr)
d_optim = torch.optim.Adam(discriminator.parameters(),lr=lr)
loss_fn = torch.nn.BCELoss()
# 绘图函数
def gen_img_plot(model,test_input):
prediction = np.squeeze(model(test_input).detach().cpu().numpy())
fig = plt.figure(figsize=(4,4))
for i in range(16):
plt.subplot(4,4,i+1)
plt.imshow((prediction[i] + 1 )/2)
plt.axis('off')
plt.show()
test_input = torch.randn(16,100,device=device)
# GAN训练
D_loss = list()
G_loss = list()
for epoch in range(epochs):
d_epoch_loss = 0
g_epoch_loss = 0
count = len(dataloader)
for step , (img,_) in enumerate(dataloader):
img = img.to(device)
size = img.size(0)
random_noise = torch.randn(size,100,device=device)
# 真实图片上的损失
d_optim.zero_grad()
real_output = discriminator(img) # 对判别器输入真实的图片,real_output 对真实图片预测的结果
# 判别器在真实图像上的损失
d_real_loss = loss_fn(real_output,torch.ones_like(real_output))
d_real_loss.backward()
# 生成图片上的损失
gen_img = generator(random_noise)
fake_output = discriminator(gen_img.detach()) # 判别器输入生成的图片,对生成图片的预测
# 得到判别器在生成图像上的损失
d_fake_loss = loss_fn(fake_output,torch.zeros_like(fake_output))
d_fake_loss.backward()
d_loss = d_real_loss + d_fake_loss
d_optim.step()
# 生成器
g_optim.zero_grad()
fake_output = discriminator(gen_img)
# 生成器的损失
g_loss = loss_fn(fake_output,torch.ones_like(fake_output))
g_loss.backward()
g_optim.step()
with torch.no_grad():
d_epoch_loss += d_loss
g_epoch_loss += g_loss
with torch.no_grad():
d_epoch_loss /= count
g_epoch_loss /= count
D_loss.append(d_epoch_loss)
G_loss.append(g_epoch_loss)
print('Epoch:',epoch)
gen_img_plot(generator,test_input)
print('D_loss:',d_epoch_loss)
print('G_loss:',g_epoch_loss)具体内容请看:https://blog.csdn.net/weixin_46034490/article/details/127036918
代码运行的结果:
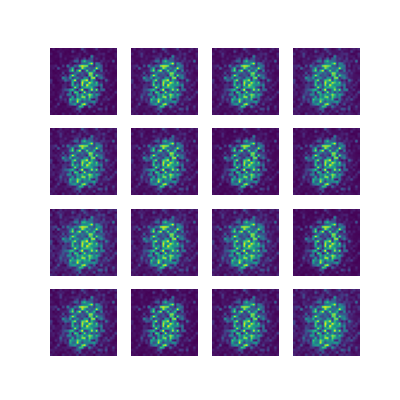
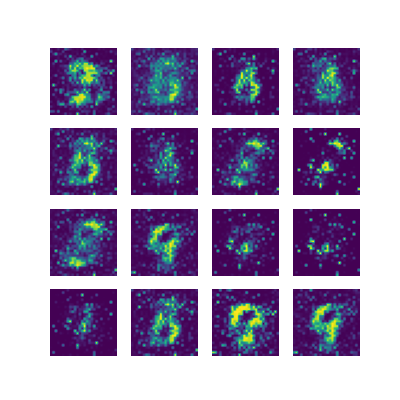
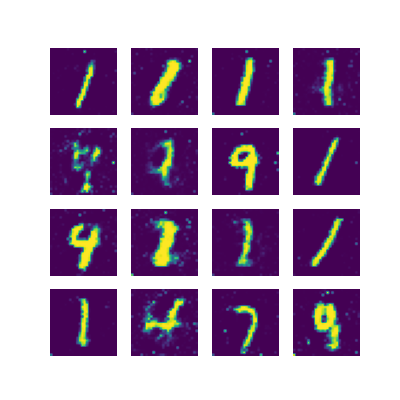
代码运行的结果也确实如这位老哥所说,GAN网络的弊端还是很明显的,多样性不足,容易模式崩溃(模式崩溃:就是生成器想着去骗判别器,结果发现了一条能一劳永逸的方法,就一直生成那种图片,就如上图一直生成1,只是因为好骗),而且不擅长处理离散数据。
#transform = transforms.Compose([...]):定义一个转换流程,它包括两个步骤。
#transforms.ToTensor():这是一个转换函数,它的作用是将PIL图像或numpy数组转换为torch.Tensor。在这个过程中,像素值也会被归一化,即除以255,使其范围在0-1之间。
#transforms.Normalize(0.5,0.5):这是一个标准化函数。这里传入的两个参数分别是均值和标准差。具体来说,此函数会将上一步得到的0-1范围的像素值进一步归一化为-1到1的范围。
#这里的像素值概念为:像素值是数字图像中每个像素的强度或颜色深度的表示。在灰度图像中,像素值通常范围在0到255之间(8位深度),其中0表示黑色,255表示白色,中间的值表示不同的灰度级别。在彩色图像中,像素值通常由一个或多个颜色通道组成,例如RGB图像由红、绿、蓝三个通道组成,每个通道的像素值范围也是0到255。
#在这段代码中,转换流程首先将PIL图像或numpy数组转换为torch.Tensor。在这个过程中,像素值也会被归一化,即除以255,使其范围在0-1之间。接下来的transforms.Normalize操作会将0-1范围内的像素值进一步归一化为-1到1的范围。这样的处理可以帮助模型更好地进行训练,因为模型的激活函数通常在这个范围内有更好的性能。
#transforms.Normalize操作会将0-1范围内的像素值进一步归一化为-1到1的范围,这样做的理由是:为了帮助模型的收敛和提高模型的训练稳定性。通过将像素值归一化为-1到1的范围,可以使模型的输入数据具有较小的幅度,这有助于减少模型训练过程中的内部协变量偏移(internal covariate shift)。内部协变量偏移是指模型训练过程中输入数据的分布发生变化,这可能导致训练不稳定或减慢收敛速度。通过归一化输入数据,可以使得模型的参数更容易适应数据的分布,从而加速训练并提高模型的性能。#train_ds = torchvision.datasets.MNIST('data',train=True, transform=transform, download=True):这行代码的目的是加载MNIST数据集的训练数据。
#上述括号内的代码解析:
'data':指定数据集保存的目录名为'data'。
train=True:表示加载的是训练数据。
transform=transform:应用之前定义的转换流程,即对每张图片进行归一化处理。
download=True:如果数据集尚未在指定的目录中,则下载数据集。#dataloader = torch.utils.data.DataLoader(train_ds,batch_size=64,shuffle=True):创建一个数据加载器。
#上述括号内的代码解析:
train_ds:之前加载的训练数据集(上面的数据集)。
batch_size=64:每个批次包含64张图片。
shuffle=True:在每个训练时代开始时,随机混洗数据。# 生成器 使用噪声来进行输入
# 输入为长度为100的 噪声 (正态分布随机数) 生成器输出为(1,28,28)的图片
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.main = nn.Sequential(
nn.Linear(100, 256),nn.ReLU(), //ReLU激活函数
nn.Linear(256, 512),nn.ReLU(), //ReLU激活函数
nn.Linear(512,28 * 28),nn.Tanh() //Tanh激活函数
)
def forward(self,x): # x 表示为长度为100 的噪声
img = self.main(x)
img = img.view(-1,28,28)
return img
#这段代码定义了一个生成器网络(Generator),该网络使用PyTorch框架实现。生成器的主要目的是通过接收随机噪声作为输入,生成新的数据样本,例如图像。
——————————————————————————————————————————————————————————————————————————————————————
#以下是代码的逐行解释:
#class Generator(nn.Module): - 定义一个名为Generator的类,该类继承自PyTorch的基础模块nn.Module。
#def __init__(self): - 初始化函数,用于设置生成器的结构。
#super(Generator, self).__init__() - 调用父类nn.Module的初始化函数。
#self.main = nn.Sequential(...) - 定义生成器的主要结构,这里使用了一个序列模型(Sequential model)。该模型包含三个全连接层(Linear layers):
#第一个全连接层将100维的输入噪声映射到256维的空间,并使用ReLU激活函数。
#第二个全连接层将256维的输入映射到512维的空间,并使用ReLU激活函数。
#第三个全连接层将512维的输入映射到28 * 28维的空间,即输出一个784维的向量,代表一张28x28的图像。然后使用Tanh激活函数,将输出值规范化到[-1, 1]的范围。
#def forward(self, x): - 定义前向传播函数,该函数接收输入噪声x。
#img = self.main(x) - 将输入噪声x传递给生成器的主要结构,得到输出图像img。
#img = img.view(-1, 28, 28) - 改变输出图像的形状,将其从[batch_size, 784]重塑为[batch_size, 28, 28],这里-1代表自动计算batch_size。
#return img - 返回生成的图像。
#综上所述,这段代码定义了一个简单的生成器网络,该网络可以将100维的正态分布噪声转换为28x28的图像。
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.main = nn.Sequential(
# 输入层到隐藏层1
nn.Linear(100, 256),
nn.ReLU(),
# 隐藏层1到隐藏层2
nn.Linear(256, 512),
nn.ReLU(),
# 隐藏层2到输出层
nn.Linear(512, 28 * 28),
nn.Tanh()
)
# 初始化权重
for m in self.main.modules():
if isinstance(m, nn.Linear):
init.normal_(m.weight, 0, 0.02)
init.constant_(m.bias, 0)
def forward(self, x): # x 表示为长度为100 的噪声
"""
前向传播函数,将噪声通过生成器网络生成图片
:param x: 输入的噪声,形状为 (batch_size, 100)
:return: 生成的图片,形状为 (batch_size, 1, 28, 28)
"""
img = self.main(x)
img = img.view(x.size(0), 1, 28, 28)
return img
#然后我给生成器加了权重比之后,发现模式崩溃的更快了:),太棒了,直接让生成器快速偷懒,一条路摸到黑,应该判别器也加东西优化一下的(
#注意给生成器加了权重之后别忘了在开头引入这两东西:
import torch.nn as nn
import torch.nn.init as init
#还有:x.size(0)中的参数0表示获取张量x的第一个维度的大小,即batch_size。在PyTorch中,张量的维度是从0开始索引的,因此第一个维度的索引是0。通过调用x.size(0),我们可以获取张量x的第一个维度的大小,即批次中样本的数量。这个值对于后续的操作非常重要,例如在展平图片时需要保持批次大小不变。因此,将size函数的参数设置为0是为了获取张量x的第一个维度的大小。# 判别器的实现 输入为一张(1,28,28)图片 输出为二分类的概率值,输出使用sigmoid激活 0-1#
# 是用BCELoss损失函数
# 判别器一般使用 LeakyReLu 激活函数
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.main = nn.Sequential(
nn.Linear(28*28,512),nn.LeakyReLU(),
nn.Linear(512,256),nn.LeakyReLU(),
nn.Linear(256,1),nn.Sigmoid()
)
def forward(self,x): # x 为一张图片
x = x.view(-1,28*28)
x = self.main(x)
return x
#这段代码定义了一个判别器(Discriminator)类,该类的结构是一个简单的三层全连接神经网络。这个判别器是用于二分类任务的,即判断输入的图片是真实的还是生成的(通常用于对抗生成网络,如GAN)。
——————————————————————————————————————————————————————————————————————————————————————
# 以下是代码的详细解释:
# class Discriminator(nn.Module): - 定义一个新的类Discriminator,它继承了PyTorch的nn.Module类。这意味着这个类可以被视为一个神经网络模型。
# def __init__(self): - 初始化函数。当创建Discriminator类的一个实例时,这个函数会被调用。
# super(Discriminator, self).__init__() - 调用父类nn.Module的初始化函数。
# self.main = nn.Sequential(...) - 定义判别器的主要结构。这是一个序贯模型,包括三个全连接层。
# nn.Linear(28*28,512) - 第一层全连接层。它接受一个形状为(batch_size, 28*28)的张量(即一批28x28的图片),并将其转换为形状为(batch_size, 512)的张量。
# nn.LeakyReLU() - 激活函数。在这里,使用了Leaky ReLU函数,它是一种修正线性单元,但在负数部分有一个小的斜率,这有助于缓解“死亡ReLU”问题。(“死亡ReLU”问题是指在神经网络训练过程中,由于参数更新不当,导致某些ReLU神经元的输入全部为负数,使得ReLU函数无法对其激活,这些神经元的参数梯度永远为0,导致在后续的训练过程中这些神经元永远不会被激活。这会导致模型学习过程中的部分数据浪费,进而影响模型的收敛速度和性能。为了解决这个问题,可以使用ReLU的变种,如Leaky ReLU或ELU等,这些激活函数在输入为负数时仍然有一定的输出,可以避免“死亡ReLU”问题的出现。)
# nn.Linear(512,256) - 第二层全连接层,将输入张量的形状从(batch_size, 512)转换为(batch_size, 256)。
# nn.Linear(256,1) - 第三层全连接层,将输入张量的形状从(batch_size, 256)转换为(batch_size, 1)。
# nn.Sigmoid() - Sigmoid激活函数,将输出值限制在0和1之间,表示二分类的概率值。
# def forward(self,x): - 前向传播函数。定义了如何将输入数据x通过模型得到输出。
# x = x.view(-1,28*28) - 重新调整输入张量x的形状。-1表示自动计算该维度的大小,以确保整个张量的元素数量不变。
# x = self.main(x) - 将调整形状后的张量x传递给判别器的主要结构(即上面定义的序贯模型)。
# return x - 返回模型的输出。
# 总的来说,这个判别器模型接受形状为(batch_size, 1, 28, 28)的图片张量作为输入,经过前向传播后,输出形状为(batch_size, 1)的二分类概率值张量。自己又去找了找别的优化方法:
# nn.Linear(28 * 28, 512),
# nn.LeakyReLU(negative_slope=0.2), # 调整负斜率
# nn.Dropout(0.3), # 添加dropout
# nn.Linear(512, 256),
# nn.LeakyReLU(negative_slope=0.2), # 调整负斜率
# nn.Dropout(0.3), # 添加dropout
# nn.Linear(256, 1),
# nn.Sigmoid()
# 激活函数负斜率调整:优化后的代码将nn.LeakyReLU()的负斜率(negative_slope)从默认的0.01调整为0.2。这个改变会使激活函数在输入值为负数时更加敏感,有助于提升模型的表达能力。
# 添加Dropout层:优化后的代码在nn.Linear()层之后添加了nn.Dropout()层,这是一种正则化手段,通过随机丢弃一部分神经元输出,可以防止模型过拟合。dropout是一种正则化技术,用于防止神经网络在训练过程中出现过拟合现象。具体来说,dropout会在每个训练批次中随机“关闭”(设置为0)一部分神经元,这意味着这些神经元在当前批次中不会起作用。这样做可以让模型不会太依赖于任何一个神经元,从而避免过拟合。在你的代码中,nn.Dropout(0.3)表示每个神经元有0.3的概率被“关闭”。注意,dropout只在训练过程中使用,测试或评估模型时通常不使用dropout。
而外知识:
激活函数ELU和激活函数ReLU的主要区别在于:
- 输出值范围:ReLU的输出值范围是[0, +∞),而ELU的输出值范围是(-α, +∞)。这意味着ELU的负值输出可以使得模型的平均输出接近零,类似于Batch Normalization的效果,但是计算量更少。
- 激活状态:ReLU在输入小于0时处于非激活状态,输出为0。而ELU在输入小于0时仍然有非零输出,这可以使得神经元在负值区域也能被激活,从而缓解梯度消失问题。
以上两点是激活函数ELU和激活函数ReLU的主要区别,具体选择哪个激活函数需要根据实际的应用场景和模型需求来决定。
然后就是模型训练设置相关的代码:
epochs = 200 //训练次数
lr = 0.001 //学习率
# lr = 0.0001
# 初始化模型
device = 'cuda' if torch.cuda.is_available() else 'cpu'
generator = Generator().to(device)
discriminator = Discriminator().to(device)
# 添加权重衰减 优化器(梯度下降)
# weight_decay = 0.001
weight_decay = 0.05 //权重衰减
g_optim = torch.optim.Adam(generator.parameters(), lr=lr, weight_decay=weight_decay)
d_optim = torch.optim.Adam(discriminator.parameters(), lr=lr, weight_decay=weight_decay)
loss_fn = torch.nn.BCELoss()学习率:控制模型参数在梯度更新时的步长。较大的学习率可能导致训练过程不稳定,而较小的学习率可能导致训练速度缓慢或陷入局部最小值。
权重衰减:是一种正则化技术,用于防止模型过拟合。它通过对模型参数施加一个惩罚项来减少过拟合。权重衰减的值越大,对参数的惩罚越重。
GAN训练
D_loss = list()
G_loss = list()
for epoch in range(epochs):
d_epoch_loss = 0
g_epoch_loss = 0
count = len(dataloader)
for step , (img,_) in enumerate(dataloader):
img = img.to(device)
size = img.size(0)
random_noise = torch.randn(size, 100, device=device)
# 真实图片上的损失
d_optim.zero_grad()
real_output = discriminator(img) # 对判别器输入真实的图片,real_output 对真实图片预测的结果
# 判别器在真实图像上的损失
d_real_loss = loss_fn(real_output,torch.ones_like(real_output))
d_real_loss.backward()
# 生成图片上的损失
gen_img = generator(random_noise)
fake_output = discriminator(gen_img.detach()) # 判别器输入生成的图片,对生成图片的预测
# 得到判别器在生成图像上的损失
d_fake_loss = loss_fn(fake_output,torch.zeros_like(fake_output))
d_fake_loss.backward()
d_loss = d_real_loss + d_fake_loss
d_optim.step()
# 生成器
g_optim.zero_grad()
fake_output = discriminator(gen_img)
# 生成器的损失
g_loss = loss_fn(fake_output,torch.ones_like(fake_output))
g_loss.backward()
g_optim.step()
with torch.no_grad():
d_epoch_loss += d_loss
g_epoch_loss += g_loss
with torch.no_grad():
d_epoch_loss /= count
g_epoch_loss /= count
D_loss.append(d_epoch_loss)
G_loss.append(g_epoch_loss)
print('Epoch:',epoch)
gen_img_plot(generator,test_input)
print('D_loss:',d_epoch_loss)
print('G_loss:',g_epoch_loss)#上述代码讲解:
#初始化两个列表 D_loss 和 G_loss 来存储每个epoch的判别器和生成器的损失。
#进行 epochs 次训练循环。
#在每个epoch内,初始化 d_epoch_loss 和 g_epoch_loss 来存储该epoch内判别器和生成器的累计损失。
#通过 dataloader 加载真实数据,并对每批数据进行训练。
#对真实图片计算判别器的损失 (d_real_loss),然后对生成器生成的假图片计算判别器的损失(d_fake_loss)。将两者相加得到判别器的总损失 (d_loss),然后进行反向传播和优化。
#对生成器生成的假图片计算生成器的损失 (g_loss),然后进行反向传播和优化。
#在每个epoch结束后,计算该epoch的平均判别器和生成器损失,并添加到 D_loss 和 G_loss 列表中。
#打印当前epoch数、判别器和生成器的损失,以及生成器生成的假图片。backward()函数
#backward() 函数是PyTorch中的一个重要函数,用于进行反向传播。反向传播是训练神经网络时的一个重要步骤,用于计算损失函数对模型参数的梯度。
#具体来说,backward() 函数会计算 d_real_loss 对计算图中所有可导参数的梯度,并将这些梯度存储在相应参数的 .grad 属性中。这些梯度信息用于后续的优化步骤,例如使用梯度下降算法更新模型的参数。
#简而言之,backward() 函数使得我们能够通过链式法则,从最终的损失函数开始,反向计算每个参数的梯度,从而进行模型的优化。zero_grid()函数
#zero_grad() 是PyTorch中的一个函数,用于将模型参数的梯度清零。在训练神经网络时,每次进行反向传播之前,通常需要调用 zero_grad() 函数来确保梯度不会累积。这是因为,如果不进行梯度清零,每次反向传播都会在已有的梯度上进行累加,这可能导致不正确的梯度更新。
#通过调用 zero_grad(),我们可以确保每次反向传播都是基于当前批次数据的梯度,而不是累积的梯度。这样可以确保模型参数的更新是准确且稳定的。下面是我自己改了改参数什么的得出来的代码:
import numpy as np
import torch
import torch.nn as nn
import torch.nn.init as init
import torch.optim as optim
import matplotlib.pyplot as plt
import torchvision
from torchvision import transforms
## 对数据做归一化 (-1 1)
transform = transforms.Compose([
transforms.ToTensor(), # 0-1 : channel,high ,witch
transforms.Normalize(0.5,0.5)
])
train_ds = torchvision.datasets.MNIST('data', train=True, transform=transform, download=True)
dataloader = torch.utils.data.DataLoader(train_ds, batch_size=64, shuffle=True)
# 生成器 使用噪声来进行输入
# 输入为长度为100的 噪声 (正态分布随机数) 生成器输出为(1,28,28)的图片
# 定义生成器类
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.main = nn.Sequential(
nn.Linear(100, 256),
nn.ReLU(), # 更改激活函数为ReLU
nn.BatchNorm1d(256),
nn.Linear(256, 512),
nn.ReLU(), # 更改激活函数为ReLU
nn.BatchNorm1d(512),
nn.Linear(512, 28 * 28),
nn.Tanh()
)
# 初始化权重
for m in self.main.modules():
if isinstance(m, nn.Linear):
init.normal_(m.weight, 0, 0.02)
init.constant_(m.bias, 0)
def forward(self, x): # x 表示为长度为100 的噪声
"""
前向传播函数,将噪声通过生成器网络生成图片
:param x: 输入的噪声,形状为 (batch_size, 100)
:return: 生成的图片,形状为 (batch_size, 1, 28, 28)
"""
img = self.main(x)
img = img.view(x.size(0), 1, 28, 28)
return img
# 判别器的实现 输入为一张(1,28,28)图片 输出为二分类的概率值,输出使用sigmoid激活 0-1#
# 是用BCELoss损失函数
# 判别器一般使用 LeakyReLu 激活函数
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.main = nn.Sequential(
nn.Linear(28 * 28, 512),
nn.LeakyReLU(negative_slope=0.2),
nn.Dropout(0.3),
nn.utils.spectral_norm(nn.Linear(512, 256)),
nn.LeakyReLU(negative_slope=0.2),
nn.Dropout(0.3),
nn.utils.spectral_norm(nn.Linear(256, 1)),
nn.Sigmoid()
)
def forward(self,x): # x 为一张图片
x = x.view(-1,28*28)
x = self.main(x)
return x
epochs = 200
lr = 0.0005
# 初始化模型
device = 'cuda' if torch.cuda.is_available() else 'cpu'
generator = Generator().to(device)
discriminator = Discriminator().to(device)
# 优化器(梯度下降)
g_optim = torch.optim.Adam(generator.parameters(),lr=lr)
d_optim = torch.optim.Adam(discriminator.parameters(),lr=lr)
loss_fn = torch.nn.BCELoss()
# 绘图函数
def gen_img_plot(model,test_input):
prediction = np.squeeze(model(test_input).detach().cpu().numpy())
fig = plt.figure(figsize=(4,4))
for i in range(16):
plt.subplot(4,4,i+1)
plt.imshow((prediction[i] + 1 )/2)
plt.axis('off')
plt.show()
test_input = torch.randn(16,100,device=device) #100代表了生成噪声向量的特征数量或维度。
# GAN训练
D_loss = list()
G_loss = list()
for epoch in range(epochs):
d_epoch_loss = 0
g_epoch_loss = 0
count = len(dataloader)
for step , (img,_) in enumerate(dataloader):
img = img.to(device)
size = img.size(0)
random_noise = torch.randn(size, 100, device=device)
# 真实图片上的损失
d_optim.zero_grad()
real_output = discriminator(img) # 对判别器输入真实的图片,real_output 对真实图片预测的结果
# 判别器在真实图像上的损失
d_real_loss = loss_fn(real_output,torch.ones_like(real_output))
d_real_loss.backward()
# 生成图片上的损失
gen_img = generator(random_noise)
fake_output = discriminator(gen_img.detach()) # 判别器输入生成的图片,对生成图片的预测
# 得到判别器在生成图像上的损失
d_fake_loss = loss_fn(fake_output,torch.zeros_like(fake_output))
d_fake_loss.backward()
d_loss = d_real_loss + d_fake_loss
d_optim.step()
# 生成器
g_optim.zero_grad()
fake_output = discriminator(gen_img)
# 生成器的损失
g_loss = loss_fn(fake_output,torch.ones_like(fake_output))
g_loss.backward()
g_optim.step()
with torch.no_grad():
d_epoch_loss += d_loss
g_epoch_loss += g_loss
with torch.no_grad():
d_epoch_loss /= count
g_epoch_loss /= count
D_loss.append(d_epoch_loss)
G_loss.append(g_epoch_loss)
print('Epoch:',epoch)
gen_img_plot(generator,test_input)
print('D_loss:',d_epoch_loss)
print('G_loss:',g_epoch_loss)
然后出来的结果:
经过优化之后得出来的GAN网络从下图可以看出来,与原码相比,该优化过之后得GAN网络在一定程度上降低了模式崩溃的概率,但代价是在一定程度上降低了生成图像的清晰度,而且相比原码的学习生成效率也几乎下降了一半,只能说为了缓解模式崩溃这个问题以我的能力只能做到这样了。过程如下:


Epoch: 0
D_loss: tensor(0.2201)
G_loss: tensor(3.8274)
Epoch: 1
D_loss: tensor(0.1984)
G_loss: tensor(3.8559)
Epoch: 2
D_loss: tensor(0.3205)
G_loss: tensor(3.2079)
Epoch: 3
D_loss: tensor(0.4869)
G_loss: tensor(2.6017)
Epoch: 4
D_loss: tensor(0.7064)
G_loss: tensor(1.9556)
Epoch: 5
D_loss: tensor(0.8974)
G_loss: tensor(1.5654)
Epoch: 6
D_loss: tensor(0.9135)
G_loss: tensor(1.5139)
Epoch: 7
D_loss: tensor(0.8715)
G_loss: tensor(1.5534)
Epoch: 8
D_loss: tensor(0.9502)
G_loss: tensor(1.4970)
Epoch: 9
D_loss: tensor(1.0074)
G_loss: tensor(1.3712)
Epoch: 10
D_loss: tensor(0.9745)
G_loss: tensor(1.3978)
Epoch: 11
D_loss: tensor(0.9934)
G_loss: tensor(1.3724)
Epoch: 12
D_loss: tensor(1.0420)
G_loss: tensor(1.3040)
Epoch: 13
D_loss: tensor(1.0889)
G_loss: tensor(1.2044)
Epoch: 14
D_loss: tensor(1.1069)
G_loss: tensor(1.1727)
Epoch: 15
D_loss: tensor(1.1114)
G_loss: tensor(1.1590)
Epoch: 16
D_loss: tensor(1.1260)
G_loss: tensor(1.1313)
Epoch: 17
D_loss: tensor(1.1439)
G_loss: tensor(1.0925)
Epoch: 18
D_loss: tensor(1.1287)
G_loss: tensor(1.1264)
Epoch: 19
D_loss: tensor(1.1542)
G_loss: tensor(1.0764)
Epoch: 20
D_loss: tensor(1.1466)
G_loss: tensor(1.0824)
Epoch: 21
D_loss: tensor(1.1679)
G_loss: tensor(1.0477)
Epoch: 22
D_loss: tensor(1.1811)
G_loss: tensor(1.0185)
Epoch: 23
D_loss: tensor(1.1892)
G_loss: tensor(1.0007)
Epoch: 24
D_loss: tensor(1.1846)
G_loss: tensor(1.0096)
Epoch: 25
D_loss: tensor(1.1885)
G_loss: tensor(1.0091)
Epoch: 26
D_loss: tensor(1.1945)
G_loss: tensor(0.9952)
Epoch: 27
D_loss: tensor(1.1951)
G_loss: tensor(0.9947)
Epoch: 28
D_loss: tensor(1.2055)
G_loss: tensor(0.9785)
Epoch: 29
D_loss: tensor(1.2101)
G_loss: tensor(0.9679)
Epoch: 30
D_loss: tensor(1.2132)
G_loss: tensor(0.9657)
Epoch: 31
D_loss: tensor(1.2158)
G_loss: tensor(0.9573)
Epoch: 32
D_loss: tensor(1.2272)
G_loss: tensor(0.9447)
Epoch: 33
D_loss: tensor(1.2249)
G_loss: tensor(0.9429)
Epoch: 34
D_loss: tensor(1.2267)
G_loss: tensor(0.9429)
Epoch: 35
D_loss: tensor(1.2268)
G_loss: tensor(0.9366)
Epoch: 36
D_loss: tensor(1.2244)
G_loss: tensor(0.9500)
Epoch: 37
D_loss: tensor(1.2283)
G_loss: tensor(0.9332)
Epoch: 38
D_loss: tensor(1.2341)
G_loss: tensor(0.9411)
Epoch: 39
D_loss: tensor(1.2332)
G_loss: tensor(0.9284)
Epoch: 40
D_loss: tensor(1.2297)
G_loss: tensor(0.9372)
Epoch: 41
D_loss: tensor(1.2230)
G_loss: tensor(0.9437)
Epoch: 42
D_loss: tensor(1.2256)
G_loss: tensor(0.9467)
Epoch: 43
D_loss: tensor(1.2265)
G_loss: tensor(0.9379)
Epoch: 44
D_loss: tensor(1.2338)
G_loss: tensor(0.9417)
Epoch: 45
D_loss: tensor(1.2302)
G_loss: tensor(0.9344)
Epoch: 46
D_loss: tensor(1.2313)
G_loss: tensor(0.9443)
Epoch: 47
D_loss: tensor(1.2298)
G_loss: tensor(0.9466)
Epoch: 48
D_loss: tensor(1.2288)
G_loss: tensor(0.9437)
Epoch: 49
D_loss: tensor(1.2288)
G_loss: tensor(0.9419)
Epoch: 50
D_loss: tensor(1.2259)
G_loss: tensor(0.9540)
Epoch: 51
D_loss: tensor(1.2253)
G_loss: tensor(0.9525)
Epoch: 52
D_loss: tensor(1.2266)
G_loss: tensor(0.9545)
Epoch: 53
D_loss: tensor(1.2244)
G_loss: tensor(0.9470)
Epoch: 54
D_loss: tensor(1.2231)
G_loss: tensor(0.9645)
Epoch: 55
D_loss: tensor(1.2211)
G_loss: tensor(0.9516)
Epoch: 56
D_loss: tensor(1.2227)
G_loss: tensor(0.9605)
Epoch: 57
D_loss: tensor(1.2220)
G_loss: tensor(0.9602)
Epoch: 58
D_loss: tensor(1.2174)
G_loss: tensor(0.9641)
Epoch: 59
D_loss: tensor(1.2229)
G_loss: tensor(0.9600)
Epoch: 60
D_loss: tensor(1.2203)
G_loss: tensor(0.9658)
Epoch: 61
D_loss: tensor(1.2164)
G_loss: tensor(0.9632)
Epoch: 62
D_loss: tensor(1.2169)
G_loss: tensor(0.9664)
Epoch: 63
D_loss: tensor(1.2115)
G_loss: tensor(0.9655)
Epoch: 64
D_loss: tensor(1.2236)
G_loss: tensor(0.9651)
Epoch: 65
D_loss: tensor(1.2184)
G_loss: tensor(0.9608)
Epoch: 66
D_loss: tensor(1.2182)
G_loss: tensor(0.9667)
Epoch: 67
D_loss: tensor(1.2174)
G_loss: tensor(0.9644)
Epoch: 68
D_loss: tensor(1.2122)
G_loss: tensor(0.9652)
Epoch: 69
D_loss: tensor(1.2170)
G_loss: tensor(0.9630)
Epoch: 70
D_loss: tensor(1.2175)
G_loss: tensor(0.9708)
Epoch: 71
D_loss: tensor(1.2191)
G_loss: tensor(0.9651)
Epoch: 72
D_loss: tensor(1.2200)
G_loss: tensor(0.9698)
Epoch: 73
D_loss: tensor(1.2167)
G_loss: tensor(0.9656)
Epoch: 74
D_loss: tensor(1.2165)
G_loss: tensor(0.9676)
Epoch: 75
D_loss: tensor(1.2196)
G_loss: tensor(0.9604)
Epoch: 76
D_loss: tensor(1.2241)
G_loss: tensor(0.9682)
Epoch: 77
D_loss: tensor(1.2166)
G_loss: tensor(0.9574)
Epoch: 78
D_loss: tensor(1.2192)
G_loss: tensor(0.9602)
Epoch: 79
D_loss: tensor(1.2180)
G_loss: tensor(0.9628)
Epoch: 80
D_loss: tensor(1.2152)
G_loss: tensor(0.9678)
Epoch: 81
D_loss: tensor(1.2147)
G_loss: tensor(0.9729)
Epoch: 82
D_loss: tensor(1.2193)
G_loss: tensor(0.9708)
Epoch: 83
D_loss: tensor(1.2192)
G_loss: tensor(0.9666)
Epoch: 84
D_loss: tensor(1.2156)
G_loss: tensor(0.9690)
Epoch: 85
D_loss: tensor(1.2145)
G_loss: tensor(0.9653)
Epoch: 86
D_loss: tensor(1.2169)
G_loss: tensor(0.9707)
Epoch: 87
D_loss: tensor(1.2191)
G_loss: tensor(0.9667)
Epoch: 88
D_loss: tensor(1.2179)
G_loss: tensor(0.9722)
Epoch: 89
D_loss: tensor(1.2142)
G_loss: tensor(0.9658)
Epoch: 90
D_loss: tensor(1.2144)
G_loss: tensor(0.9727)
Epoch: 91
D_loss: tensor(1.2120)
G_loss: tensor(0.9752)
Epoch: 92
D_loss: tensor(1.2145)
G_loss: tensor(0.9723)
Epoch: 93
D_loss: tensor(1.2167)
G_loss: tensor(0.9763)
Epoch: 94
D_loss: tensor(1.2173)
G_loss: tensor(0.9647)
Epoch: 95
D_loss: tensor(1.2147)
G_loss: tensor(0.9769)
Epoch: 96
D_loss: tensor(1.2124)
G_loss: tensor(0.9687)
Epoch: 97
D_loss: tensor(1.2131)
G_loss: tensor(0.9785)
Epoch: 98
D_loss: tensor(1.2137)
G_loss: tensor(0.9681)
Epoch: 99
D_loss: tensor(1.2132)
G_loss: tensor(0.9811)
Epoch: 100
D_loss: tensor(1.2120)
G_loss: tensor(0.9750)
Epoch: 101
D_loss: tensor(1.2119)
G_loss: tensor(0.9747)
Epoch: 102
D_loss: tensor(1.2109)
G_loss: tensor(0.9754)
Epoch: 103
D_loss: tensor(1.2107)
G_loss: tensor(0.9794)
Epoch: 104
D_loss: tensor(1.2134)
G_loss: tensor(0.9767)
Epoch: 105
D_loss: tensor(1.2126)
G_loss: tensor(0.9773)
Epoch: 106
D_loss: tensor(1.2121)
G_loss: tensor(0.9727)
Epoch: 107
D_loss: tensor(1.2079)
G_loss: tensor(0.9825)
Epoch: 108
D_loss: tensor(1.2110)
G_loss: tensor(0.9791)
Epoch: 109
D_loss: tensor(1.2108)
G_loss: tensor(0.9783)
Epoch: 110
D_loss: tensor(1.2080)
G_loss: tensor(0.9808)
Epoch: 111
D_loss: tensor(1.2056)
G_loss: tensor(0.9797)
Epoch: 112
D_loss: tensor(1.2090)
G_loss: tensor(0.9826)
Epoch: 113
D_loss: tensor(1.2071)
G_loss: tensor(0.9871)
Epoch: 114
D_loss: tensor(1.2092)
G_loss: tensor(0.9848)
Epoch: 115
D_loss: tensor(1.2069)
G_loss: tensor(0.9880)
Epoch: 116
D_loss: tensor(1.2087)
G_loss: tensor(0.9836)
Epoch: 117
D_loss: tensor(1.2049)
G_loss: tensor(0.9880)
Epoch: 118
D_loss: tensor(1.2126)
G_loss: tensor(0.9876)
Epoch: 119
D_loss: tensor(1.2099)
G_loss: tensor(0.9800)
Epoch: 120
D_loss: tensor(1.2140)
G_loss: tensor(0.9846)
Epoch: 121
D_loss: tensor(1.2099)
G_loss: tensor(0.9815)
Epoch: 122
D_loss: tensor(1.2025)
G_loss: tensor(0.9891)
Epoch: 123
D_loss: tensor(1.2092)
G_loss: tensor(0.9866)
Epoch: 124
D_loss: tensor(1.2111)
G_loss: tensor(0.9825)
Epoch: 125
D_loss: tensor(1.2083)
G_loss: tensor(0.9846)
Epoch: 126
D_loss: tensor(1.2086)
G_loss: tensor(0.9893)
Epoch: 127
D_loss: tensor(1.2070)
G_loss: tensor(0.9871)
Epoch: 128
D_loss: tensor(1.2084)
G_loss: tensor(0.9847)
Epoch: 129
D_loss: tensor(1.2085)
G_loss: tensor(0.9887)
Epoch: 130
D_loss: tensor(1.2085)
G_loss: tensor(0.9854)
Epoch: 131
D_loss: tensor(1.2071)
G_loss: tensor(0.9823)
Epoch: 132
D_loss: tensor(1.2050)
G_loss: tensor(0.9918)
Epoch: 133
D_loss: tensor(1.2065)
G_loss: tensor(0.9852)
Epoch: 134
D_loss: tensor(1.2067)
G_loss: tensor(0.9860)
Epoch: 135
D_loss: tensor(1.2138)
G_loss: tensor(0.9836)
Epoch: 136
D_loss: tensor(1.2120)
G_loss: tensor(0.9825)
Epoch: 137
D_loss: tensor(1.2110)
G_loss: tensor(0.9774)
Epoch: 138
D_loss: tensor(1.2142)
G_loss: tensor(0.9795)
Epoch: 139
D_loss: tensor(1.2092)
G_loss: tensor(0.9838)
Epoch: 140
D_loss: tensor(1.2074)
G_loss: tensor(0.9838)
Epoch: 141
D_loss: tensor(1.2073)
G_loss: tensor(0.9823)
Epoch: 142
D_loss: tensor(1.2086)
G_loss: tensor(0.9878)
Epoch: 143
D_loss: tensor(1.2080)
G_loss: tensor(0.9879)
Epoch: 144
D_loss: tensor(1.2077)
G_loss: tensor(0.9869)
Epoch: 145
D_loss: tensor(1.2113)
G_loss: tensor(0.9863)
Epoch: 146
D_loss: tensor(1.2095)
G_loss: tensor(0.9824)
Epoch: 147
D_loss: tensor(1.2116)
G_loss: tensor(0.9858)
Epoch: 148
D_loss: tensor(1.2126)
G_loss: tensor(0.9730)
Epoch: 149
D_loss: tensor(1.2153)
G_loss: tensor(0.9826)
Epoch: 150
D_loss: tensor(1.2101)
G_loss: tensor(0.9739)
Epoch: 151
D_loss: tensor(1.2109)
G_loss: tensor(0.9859)
Epoch: 152
D_loss: tensor(1.2139)
G_loss: tensor(0.9845)
Epoch: 153
D_loss: tensor(1.2112)
G_loss: tensor(0.9795)
Epoch: 154
D_loss: tensor(1.2167)
G_loss: tensor(0.9801)
Epoch: 155
D_loss: tensor(1.2078)
G_loss: tensor(0.9773)
Epoch: 156
D_loss: tensor(1.2057)
G_loss: tensor(0.9837)
Epoch: 157
D_loss: tensor(1.2106)
G_loss: tensor(0.9885)
Epoch: 158
D_loss: tensor(1.2123)
G_loss: tensor(0.9802)
Epoch: 159
D_loss: tensor(1.2124)
G_loss: tensor(0.9791)
Epoch: 160
D_loss: tensor(1.2136)
G_loss: tensor(0.9804)
Epoch: 161
D_loss: tensor(1.2123)
G_loss: tensor(0.9770)
Epoch: 162
D_loss: tensor(1.2106)
G_loss: tensor(0.9855)
Epoch: 163
D_loss: tensor(1.2140)
G_loss: tensor(0.9829)
Epoch: 164
D_loss: tensor(1.2077)
G_loss: tensor(0.9794)
Epoch: 165
D_loss: tensor(1.2135)
G_loss: tensor(0.9806)
Epoch: 166
D_loss: tensor(1.2138)
G_loss: tensor(0.9799)
Epoch: 167
D_loss: tensor(1.2107)
G_loss: tensor(0.9798)
Epoch: 168
D_loss: tensor(1.2168)
G_loss: tensor(0.9842)
Epoch: 169
D_loss: tensor(1.2067)
G_loss: tensor(0.9705)
Epoch: 170
D_loss: tensor(1.2145)
G_loss: tensor(0.9840)
Epoch: 171
D_loss: tensor(1.2105)
G_loss: tensor(0.9797)
Epoch: 172
D_loss: tensor(1.2143)
G_loss: tensor(0.9877)
Epoch: 173
D_loss: tensor(1.2088)
G_loss: tensor(0.9783)
Epoch: 174
D_loss: tensor(1.2143)
G_loss: tensor(0.9797)
Epoch: 175
D_loss: tensor(1.2105)
G_loss: tensor(0.9780)
Epoch: 176
D_loss: tensor(1.2106)
G_loss: tensor(0.9893)
Epoch: 177
D_loss: tensor(1.2092)
G_loss: tensor(0.9811)
Epoch: 178
D_loss: tensor(1.2127)
G_loss: tensor(0.9802)
Epoch: 179
D_loss: tensor(1.2145)
G_loss: tensor(0.9847)
Epoch: 180
D_loss: tensor(1.2059)
G_loss: tensor(0.9816)
Epoch: 181
D_loss: tensor(1.2152)
G_loss: tensor(0.9859)
Epoch: 182
D_loss: tensor(1.2059)
G_loss: tensor(0.9863)
Epoch: 183
D_loss: tensor(1.2071)
G_loss: tensor(0.9832)
Epoch: 184
D_loss: tensor(1.2127)
G_loss: tensor(0.9904)
Epoch: 185
D_loss: tensor(1.2089)
G_loss: tensor(0.9854)
Epoch: 186
D_loss: tensor(1.2094)
G_loss: tensor(0.9871)
Epoch: 187
D_loss: tensor(1.2062)
G_loss: tensor(0.9881)
Epoch: 188
D_loss: tensor(1.2095)
G_loss: tensor(0.9860)
Epoch: 189
D_loss: tensor(1.2087)
G_loss: tensor(0.9894)
Epoch: 190
D_loss: tensor(1.2028)
G_loss: tensor(0.9861)
Epoch: 191
D_loss: tensor(1.2071)
G_loss: tensor(0.9891)
Epoch: 192
D_loss: tensor(1.2049)
G_loss: tensor(0.9892)
Epoch: 193
D_loss: tensor(1.2092)
G_loss: tensor(0.9832)
Epoch: 194
D_loss: tensor(1.2108)
G_loss: tensor(0.9841)
Epoch: 195
D_loss: tensor(1.2097)
G_loss: tensor(0.9875)
Epoch: 196
D_loss: tensor(1.2082)
G_loss: tensor(0.9772)
Epoch: 197
D_loss: tensor(1.2089)
G_loss: tensor(0.9846)
Epoch: 198
D_loss: tensor(1.2096)
G_loss: tensor(0.9830)
Epoch: 199
D_loss: tensor(1.2126)
G_loss: tensor(0.9881)
 RoLingG | 博客
RoLingG | 博客
评论(0)