每日算法 | 222.完全二叉树节点数计算

例题：LeetCode 上 222. 完全二叉树的节点个数

我们先来明确一下中文意境下的完全二叉树：

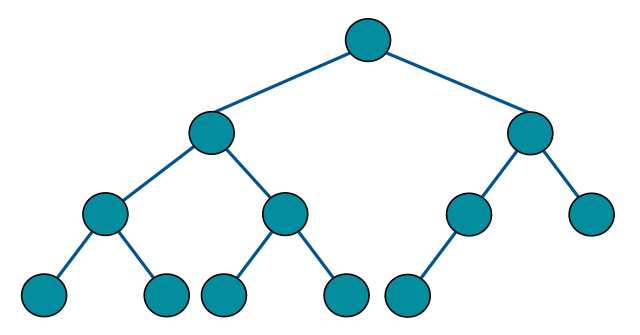
完全二叉树是一种特殊的二叉树，其中除了最后一层外，每一层的节点都尽可能地填满，且最后一层的节点都尽量靠左排列。如果完全二叉树的深度为 h，则最后一层的节点数目在 1 到 2^h 之间，并且除了最后一层外，其他每一层都被完全填满。

在我们初步理解完全二叉树之后，我们来把它和满二叉树进行区分：

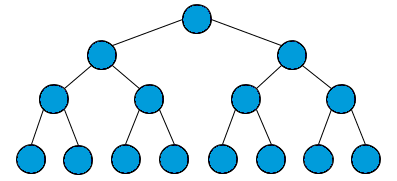
满二叉树即每个非叶子节点都有两个子节点，且所有叶子节点都在同一层上。每一层的节点数都达到最大可能值。具体而言，如果满二叉树的深度为 h，则其总节点数为 2^h - 1。
也就意味着满二叉树的结构非常规整，节点数量达到最大，且没有空缺。

我们去了解这两个树结构的区分主要作用是更好的去理解完全二叉树在普通二叉树与满二叉树之间有什么关系。这样做的好处就是能从这两个树结构的代码中提取思路。

接下来，我们就来看看如何计算一棵完全二叉树的节点数。(所有代码段都基于实现了二叉树定义的基础上进行)

如果是一个普通二叉树，显然只要向下面这样遍历一边即可，时间复杂度 O(N)：

public int countNodes(TreeNode root) {
    if (root == null) return 0;
    return 1 + countNodes(root.left) + countNodes(root.right);
}

但如果是一棵满的二叉树，用普通二叉树的计算方式显得复杂了一些，于是就有了下面这个优化代码：

public int countNodes(TreeNode root) {
    int h = 0;
    // 计算树的高度
    while (root != null) {
        root = root.left;
        h++;
    }
    // 节点总数就是 2^h - 1
    return (int)Math.pow(2, h) - 1;
}

正如我们前面了解到的满二叉树的结构特征：如果满二叉树的深度为 h，则其总节点数为 2^h - 1。

这段代码就很好的利用了满二叉树节点总数就和树的高度呈指数关系这一点进行了优化。

回过头来我们再来看完全二叉树，你结合普通二叉树和满二叉树的了解去分解完全二叉树的结构就会发现：实际上完全二叉树就是由普通二叉树和满二叉树构成的。这也就意味着我们可以将普通二叉树和满二叉树的思维重复利用在完全二叉树中。

于是我们得出了下面这段代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        TreeNode l = root;
        TreeNode r = root;
        int hl = 0;
        int hr = 0;
        while (l != null) {
            l = l.left;
            hl++;
        }
        while (r != null) {
            r = r.right;
        }
        if (hl == hr) {
            return (int)Math.pow(2, hl) - 1;
        }
        return 1 + countNodes(root.left) + countNodes(root.right);
    }
}

复杂度这些我还不太懂，现阶段只能理解理解这些算法代码的思路，日后会学习并补齐复杂度这一块。（可能吧=v=）

补充

做完题之后发现 LeetCoude 上有用 DFS 的解法，在理解代码之前我们先来了解一下 DFS 是什么。

DFS，即深度优先搜索（Depth-First Search），是一种用于遍历或搜索树或图的算法。

之前222题的解法：

class Solution {
    public int countNodes(TreeNode root) {
        return dfs(root);
    }

    private int dfs(TreeNode node) {
        if (node == null) return 0;
        return dfs(node.left) + dfs(node.right) + 1;
    }
}

其实发现还是如 labuladong说过的树结构解法的特点，无非就是遍历的基础上玩花活。

我们运行会发现 DFS 的方法要比之前那段代码快，我们就来分析一下原因：

其实主要问题在于：

之前的代码是判断是否为满二叉树时会优先计算出左右子树的高度，而不是直接遍历所有的节点。这样做的目的是为了通过比较左右子树的高度来判断是否为满二叉树，从而直接计算出节点数量。

而深度优先搜索的方法则是直接遍历所有的节点，逐个计算节点数量。

所以在完全二叉树的情况下，两种方法的效率可能相差无几，但在其他类型的二叉树或者节点数较多的情况下，第二段代码可能会更快一些，因为它能够利用树的特性来减少不必要的遍历。
但222题的代码示例相对来说是节点数较少的完全二叉树，所以简单粗暴的 DFS 会比之前那段需要更多计算的代码要快一些。

以上代码思路都是基于 labuladong 如何计算完全二叉树的节点数进行学习与理解，仅仅作为学习分享与思路理解，如果有出警问题本人立刻投降。

[算法学习] 完全二叉树节点计算

每日算法 | 222.完全二叉树节点数计算

补充

评论(0)