每日算法 区间加法②

例题：区间加法 II

题目描述：

给你一个 m x n 的矩阵 M 和一个操作数组 op 。矩阵初始化时所有的单元格都为 0 。ops[i] = [ai, bi] 意味着当所有的 0 <= x < ai 和 0 <= y < bi 时， M[x][y] 应该加 1。

在 执行完所有操作后 ，计算并返回 矩阵中最大整数的个数 。

例如：

输入: m = 3, n = 3，ops = [[2,2],[3,3]]
输出: 4
解释: M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。

代码：

class Solution {
    public int maxCount(int m, int n, int[][] ops) {
        int minrow = m;
        int mincol = n;
        for (int[]op : ops) {
            minrow = Math.min(minrow, op[0]);
            mincol = Math.min(mincol, op[1]);
        }
        return minrow * mincol;
    }
}

思路：其实这道题题目写的有种看懂非懂的感觉，但是根据题目给的示例图，我们就大概能懂到底啥意思。

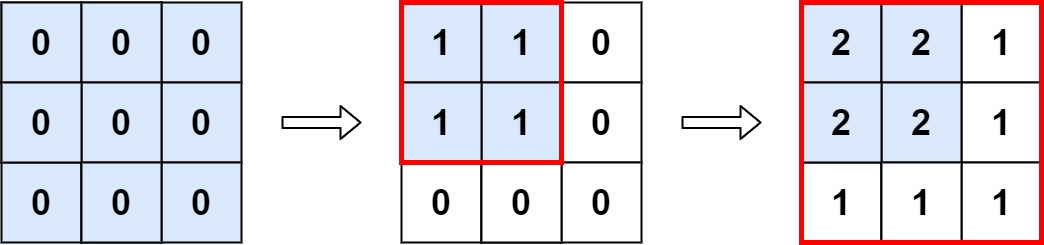
示例图的输入是题目描述的输入，我们可以清楚地看到，其实这题就是计算出矩阵内最大值的数量。这题之所以是简单题的原因就在于ops范围内一定会有[0][0]这个值的变化，无论ops内的二维矩阵有多大，一定会有[0][0]。

所以就会有个规律，ops内变化二维矩阵的范围一定是[0][0]起头，[x][y]结尾（这里的x、y泛指二维矩阵的大小，例如示例输入里的ops第一个是[2][2]，那x=2,y=2）。

综上我们就可以看出来实际上这道题就是求ops内的二维矩阵x、y取得的最小值组成的二维矩阵大小，这个由最小值组成的二维矩阵就是这个大矩阵去同一最大值的矩阵的范围。

而要计算这个矩阵中最大值的个数，即是算这个最小值组成的二维矩阵的大小值x*y。

具体过程：

输入: m = 3, n = 3，ops = [[2,2],[3,3]]

那么代码的初始化变量：

• minrow = 3（初始值，与输入的m相同）
• mincol = 3初始值，与输入的n相同）

遍历ops数组：

• 遍历第一个操作[2,2]

  • minrow更新为Math.min(3, 2)，即minrow = 2
  • mincol更新为Math.min(3, 2)，即mincol = 2

• 遍历第二个操作[3,3]

  • minrow更新为Math.min(2, 3)，即minrow仍然是2
  • minb更新为Math.min(2, 3)，即mincol仍然是2

得出最小值组成的二维矩阵后，接下来就是算x*y了。

• return minrow * mincol就同等于2 * 2 = 4